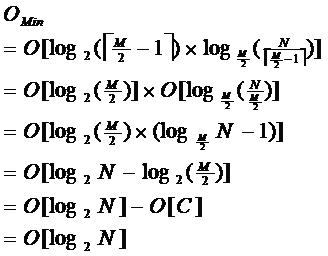B树是一种平衡的多路查找树,一般应用在内存与外存需要频繁交换的场合。
例如,在一个典型的B树的应用中,要处理的硬盘的数据量很大,无法一次全部装入内存。因此我们会使用B树,并且使B树的阶数 (节点的个数)与硬盘存储的页面大小相匹配,即一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入。
为了达到这个目的,每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个node只需一次I/O。
比如一颗b树的阶数为1001(即1个节点包含1000个关键字),高度为3,它可以储存超过10亿个关键字,我们只需要让根节点持续的留在内存中,那么在这棵树上,寻找某一个关键字至多需要两次硬盘的读取即可。
B+树主要应用在带有范围的查找。B+树和B树的主要区别在于:
- 有n棵子树的节点包含n个关键字
- 所有的叶子节点包含全部关键字的信息,及指向含这些关键字记录的指针
- 所有的非叶子节点可以看成是索引
例如节点35储存在页面1,节点123储存在页面2,节点45储存在页面3,节点67储存在页面4
当需要查找关键字1-5的节点时,B树处理按照以下步骤:
- 先索引到页面2
- 然后回到页面1
- 再索引到页面3
而B+树的处理是:
- 索引到页面2
- 直接根据指针索引到页面3
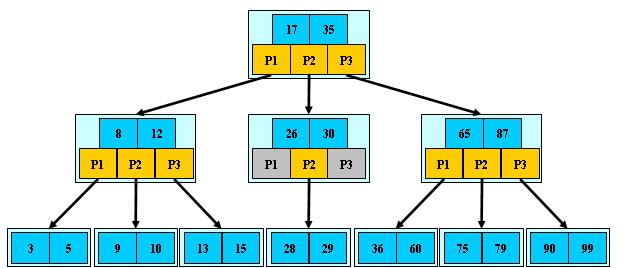
B树
是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
如:(M=3)
树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果
命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为
空,或已经是叶子结点;
B树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少
利用率,其最底搜索性能为:
其中,M为设定的非叶子结点最多子树个数,N为关键字总数;
所以B树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;
由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占
M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并;
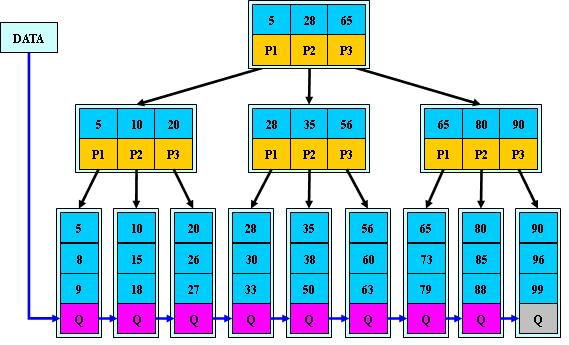
B+树
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
如:(M=3)
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在
非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统;
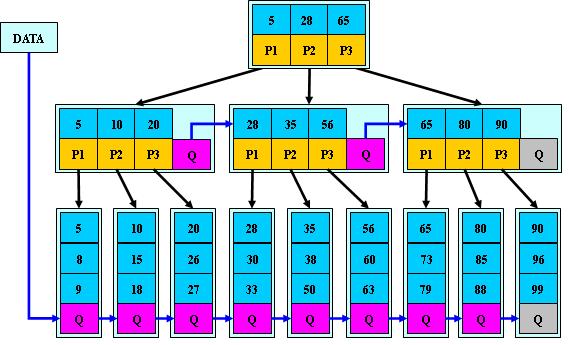
B*树
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3
(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据
复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父
结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分
数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字
(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之
间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;